Tanveer Khan Data Scientist @ NextGen Invent | Research Scholar @ Jamia Millia Islamia
Exploring decision tree based Iterative Dichotomiser 3 (ID3) algorithm
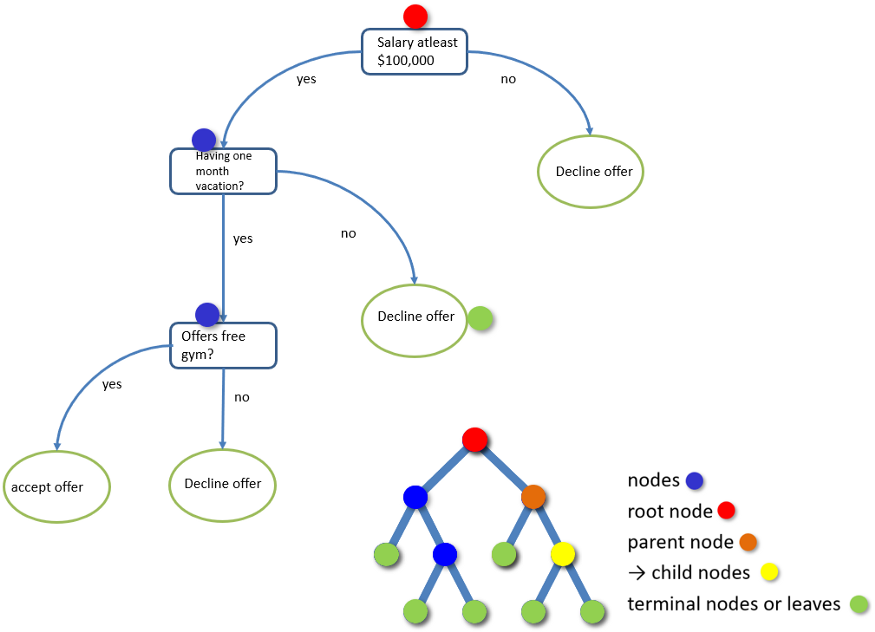
Decision trees are supervised learning algorithms used for both, classification and regression tasks. Decision trees are assigned to the information based learning algorithms which use different measures of information gain for learning. We can use decision trees for issues where we have continuous but also categorical input and target features. A decision tree has following components:
- Root Node: This attribute is used for dividing the data into two or more sets. The feature attribute in this node is selected based on Attribute Selection Techniques.
- Branch or Sub-Tree: A part of the entire decision tree is called a branch or sub-tree.
- Splitting: Dividing a node into two or more sub-nodes based on if-else conditions.
- Decision Node: After splitting the sub-nodes into further sub-nodes, then it is called the decision node.
- Leaf or Terminal Node: This is the end of the decision tree where it cannot be split into further sub-nodes.
- Pruning: Removing a sub-node from the tree is called pruning.
Figure below shows an example of a decision tree.
Iterative Dichotomiser 3 (ID3) Algorithm
ID3 (Iterative Dichotomiser 3) was developed in 1986 by Ross Quinlan. The algorithm creates a multiway tree, finding for each node (i.e. in a greedy manner) the categorical feature that will yield the largest information gain for categorical targets. Trees are grown to their maximum size and then a pruning step is usually applied to improve the ability of the tree to generalise to unseen data. ID3 relies on Information Gain (IG) and Entropy(H) values of its attributes for making predictions.
Information Gain
Information Gain IG(A,S) tells us how much uncertainty in S was reduced after splitting set S on attribute A. The mathematical formula for the Information Gain calculation per feature is:
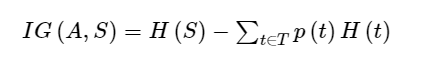
Where,
- H(S) - Entropy of set S.
- T - The subsets created from splitting set S by attribute A
- p(t) - The proportion of the number of elements in t to the number of elements in set S.
- H(t) - Entropy of subset t.
In ID3, information gain can be calculated (instead of entropy) for each remaining attribute. The attribute with the largest information gain is used to split the set S on that particular iteration.
Entropy
Entropy is a measure of the amount of uncertainty in the dataset S. The mathematical formula for the Entropy calculation for all of its categorical values is:
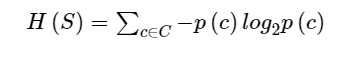
Where,
- S - The current dataset for which entropy is being calculated(changes every iteration of the ID3 algorithm).
- C - Set of classes in S {example - C ={yes, no}}
- p(c) - The proportion of the number of elements in class c to the number of elements in set S.
In ID3, entropy is calculated for each remaining attribute. The attribute with the smallest entropy is used to split the set S on that particular iteration. Entropy = 0 implies it is of pure class, that means all are of same category.
Working of ID3 Algorithm
The main idea of ID3 is to find those descriptive features which contain the most
"information" regarding the target feature and then split the dataset along the values of these features such that the target feature values for the resulting sub_datasets
are as pure as possible such descriptive feature that leaves the target feature most purely are said to be the most informative one.
This process of finding the "most informative" feature is done until we accomplish a stopping criteria where we then finally end up in so called leaf nodes.
The leaf nodes contain the predictions we will make for new query instances presented to our trained model.
Steps involved in ID3 Algorithm
The steps in ID3 algorithm are as follows:
- Step 1: Calculate entropy for the whole dataset.
- Step 2: For each attribute:
- Calculate entropy for all its categorical values.
- Calculate information gain for the feature.
- Step 3: Find the feature with maximum information gain.
- Step 4: Repeat till algorithm converges for a decision tree.
Implementation of ID3 algorithm in python
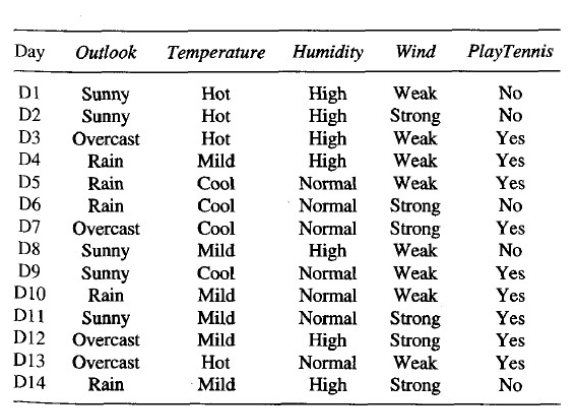
In this section we will use the ID3 algorithm to predict if we play tennis given the weather conditions we have. Figure below shows the screenshot of the weather dataset for the same.
Code for ID3 algorithm
# ID3 (Iterative Dichotomiser 3) Algorithm
import math
from collections import deque
class Node:
"""Contains the information of the node and another nodes of the Decision Tree."""
def __init__(self):
self.value = None
self.next = None
self.childs = None
class DecisionTreeClassifier:
"""Decision Tree Classifier using ID3 algorithm."""
def __init__(self, X, feature_names, labels):
self.X = X
self.feature_names = feature_names
self.labels = labels
self.labelCategories = list(set(labels))
self.labelCategoriesCount = [list(labels).count(x) for x in self.labelCategories]
self.node = None
self.entropy = self._get_entropy([x for x in range(len(self.labels))]) # calculates the initial entropy
def _get_entropy(self, x_ids):
""" Calculates the entropy.
Parameters
__________
:param x_ids: list, List containing the instances ID's
__________
:return: entropy: float, Entropy.
"""
# sorted labels by instance id
labels = [self.labels[i] for i in x_ids]
# count number of instances of each category
label_count = [labels.count(x) for x in self.labelCategories]
# calculate the entropy for each category and sum them
entropy = sum([-count / len(x_ids) * math.log(count / len(x_ids), 2) if count else 0 for count in label_count])
return entropy
def _get_information_gain(self, x_ids, feature_id):
"""Calculates the information gain for a given feature based on its entropy and the total entropy of the system.
Parameters
__________
:param x_ids: list, List containing the instances ID's
:param feature_id: int, feature ID
__________
:return: info_gain: float, the information gain for a given feature.
"""
# calculate total entropy
info_gain = self._get_entropy(x_ids)
# store in a list all the values of the chosen feature
x_features = [self.X[x][feature_id] for x in x_ids]
# get unique values
feature_vals = list(set(x_features))
# get frequency of each value
feature_vals_count = [x_features.count(x) for x in feature_vals]
# get the feature values ids
feature_vals_id = [
[x_ids[i]
for i, x in enumerate(x_features)
if x == y]
for y in feature_vals
]
# compute the information gain with the chosen feature
info_gain = info_gain - sum([val_counts / len(x_ids) * self._get_entropy(val_ids)
for val_counts, val_ids in zip(feature_vals_count, feature_vals_id)])
return info_gain
def _get_feature_max_information_gain(self, x_ids, feature_ids):
"""Finds the attribute/feature that maximizes the information gain.
Parameters
__________
:param x_ids: list, List containing the samples ID's
:param feature_ids: list, List containing the feature ID's
__________
:returns: string and int, feature and feature id of the feature that maximizes the information gain
"""
# get the entropy for each feature
features_entropy = [self._get_information_gain(x_ids, feature_id) for feature_id in feature_ids]
# find the feature that maximises the information gain
max_id = feature_ids[features_entropy.index(max(features_entropy))]
return self.feature_names[max_id], max_id
def id3(self):
"""Initializes ID3 algorithm to build a Decision Tree Classifier.
:return: None
"""
x_ids = [x for x in range(len(self.X))]
feature_ids = [x for x in range(len(self.feature_names))]
self.node = self._id3_recv(x_ids, feature_ids, self.node)
print('')
def _id3_recv(self, x_ids, feature_ids, node):
"""ID3 algorithm. It is called recursively until some criteria is met.
Parameters
__________
:param x_ids: list, list containing the samples ID's
:param feature_ids: list, List containing the feature ID's
:param node: object, An instance of the class Nodes
__________
:returns: An instance of the class Node containing all the information of the nodes in the Decision Tree
"""
if not node:
node = Node() # initialize nodes
# sorted labels by instance id
labels_in_features = [self.labels[x] for x in x_ids]
# if all the example have the same class (pure node), return node
if len(set(labels_in_features)) == 1:
node.value = self.labels[x_ids[0]]
return node
# if there are not more feature to compute, return node with the most probable class
if len(feature_ids) == 0:
node.value = max(set(labels_in_features), key=labels_in_features.count) # compute mode
return node
# else...
# choose the feature that maximizes the information gain
best_feature_name, best_feature_id = self._get_feature_max_information_gain(x_ids, feature_ids)
node.value = best_feature_name
node.childs = []
# value of the chosen feature for each instance
feature_values = list(set([self.X[x][best_feature_id] for x in x_ids]))
# loop through all the values
for value in feature_values:
child = Node()
child.value = value # add a branch from the node to each feature value in our feature
node.childs.append(child) # append new child node to current node
child_x_ids = [x for x in x_ids if self.X[x][best_feature_id] == value]
if not child_x_ids:
child.next = max(set(labels_in_features), key=labels_in_features.count)
print('')
else:
if feature_ids and best_feature_id in feature_ids:
to_remove = feature_ids.index(best_feature_id)
feature_ids.pop(to_remove)
# recursively call the algorithm
child.next = self._id3_recv(child_x_ids, feature_ids, child.next)
return node
def printTree(self):
if not self.node:
return
nodes = deque()
nodes.append(self.node)
while len(nodes) > 0:
node = nodes.popleft()
print(node.value)
if node.childs:
for child in node.childs:
print('({})'.format(child.value))
nodes.append(child.next)
elif node.next:
print(node.next)
Implementing ID3 on weather data
import numpy as np
import pandas as pd
from collections import deque
# generate weather data
# define features and target values
outlook = 'overcast,overcast,overcast,overcast,rainy,rainy,rainy,rainy,rainy,sunny,sunny,sunny,sunny,sunny'.split(',')
temp = 'hot,cool,mild,hot,mild,cool,cool,mild,mild,hot,hot,mild,cool,mild'.split(',')
humidity = 'high,normal,high,normal,high,normal,normal,normal,high,high,high,high,normal,normal'.split(',')
windy = 'FALSE,TRUE,TRUE,FALSE,FALSE,FALSE,TRUE,FALSE,TRUE,FALSE,TRUE,FALSE,FALSE,TRUE'.split(',')
play = 'yes,yes,yes,yes,yes,yes,no,yes,no,no,no,no,yes,yes'.split(',')
dataset ={'outlook':outlook,'temp':temp,'humidity':humidity,'windy':windy,'play':play}
df = pd.DataFrame(dataset,columns=['outlook','temp','humidity','windy','play'])
df.head()
# separate target from predictors
X = np.array(df.drop('play', axis=1).copy())
y = np.array(df['play'].copy())
feature_names = list(df.keys())[:4]
# import and instantiate our DecisionTreeClassifier class
from ID3 import DecisionTreeClassifier
# instantiate DecisionTreeClassifier
tree_clf = DecisionTreeClassifier(X=X, feature_names=feature_names, labels=y)
print("System entropy {:.4f}".format(tree_clf.entropy))
# run algorithm id3 to build a tree
tree_clf.id3()
tree_clf.printTree()
Results
Figure below shows the obtained results after applying ID3 algorithm on the weather data.
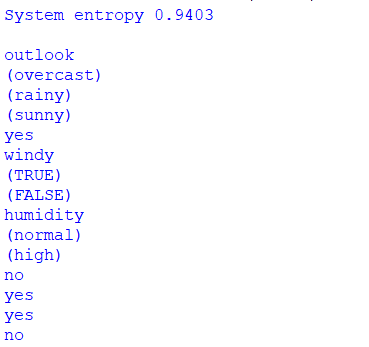
Here, in results the system entropy obtained is 0.9403 and the attribute with maximum information gain is "Outlook" thereby making it a root node.
Figure below shows the obtained decision tree for the prediciton of playing tennis based on the weather conditions.
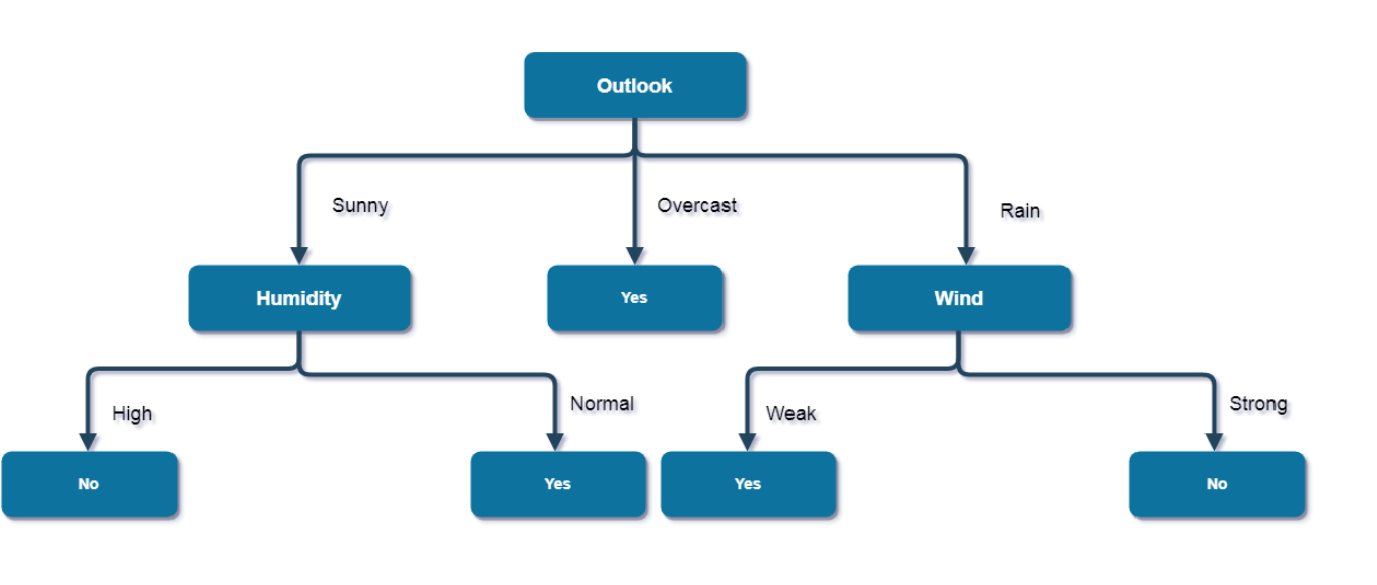
Here, when "Outlook = Rain" and "Wind = Strong", it is a pure class of category "no". And when "Outlook = Rain" and "Wind = Weak", it is again a pure class of category "yes". The figure plotted above is the final desired decision tree for our given weather dataset.
Conclusion
In this post we discussed how a decision tree based ID3 algorithm can be used for prediction purpose. ID3 builds a short tree in relatively small time and it only needs to test enough attributes until all data is classified. ID3 is easy to implement and have high generalizability.
However ID3 algorithm suffer from issues like, data may be over-fitted or over-classified, if a small sample is tested. and only one attribute at a time is tested for making a decision. Continuous and missing values are not handled properly in ID3. Thus, for this purpose advanced versions of ID3, that are C4.5 and C5.0 were introduced later by Ross Quinlan.
References
- Chai, R. M., & Wang, M. (2010, April). A more efficient classification scheme for ID3. In 2010 2nd International Conference on Computer Engineering and Technology (Vol. 1, pp. V1-329). IEEE.
- Wang, Y., Li, Y., Song, Y., Rong, X., & Zhang, S. (2017). Improvement of ID3 algorithm based on simplified information entropy and coordination degree. Algorithms, 10(4), 124.
- Pang, S. L., & Gong, J. Z. (2009). C5. 0 classification algorithm and application on individual credit evaluation of banks. Systems Engineering-Theory & Practice, 29(12), 94-104.